Study Set: +15 Math Questions for SAT Prep - Group 2

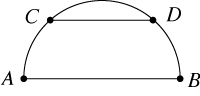
The semicircle above has a radius of r inches, and chord CD is parallel to the diameter AB. If the length of CD is (2/3) of the length of AB what is the distance between the chord and the diameter in terms of r?

Select the Correct Answer:

(1/3)πr

(2/3)πr

((2^0.5)/2)r

((5^0.5)/3)r

Correct Choice:

((5^0.5)/3)r

Choice D is correct. This represents the length of the distance between the chord and the diameter, using a radius of the circle to create a triangle, and then the Pythagorean theorem to solve correctly:(r^2)=(x^2)+((2r/3)^2) where r represents the radius of the circle and x represents the distance between the chord and the diameter.

Choice A is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have tried to use the circumference formula to determine the distance rather than making use of the radius of the circle to create a triangle.

Choice B is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have tried to use the circumference formula to determine the distance rather than making use of the radius of the circle to create a triangle.

Choice C is not the correct answer. It does not represent the length of the distance between the chord and the diameter. The student who selects this answer may have made a triangle within the circle, using a radius to connect the chord and the diameter, but then may have mistaken the triangle for a 45-45-90 triangle and tried to use this relationship to determine the distance.

Comments:

+15 Math Questions for SAT Prep - Group 2

Start Reading