Study Set Content:
Line straight ell is graphed in the xy-plane below.
If line straight ell is translated up 5 units and right 7 units, then what is the slope of the new line?
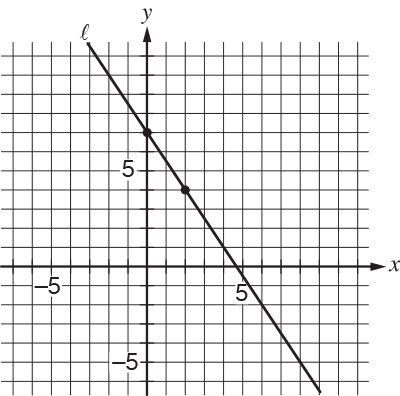
Select the Correct Answer:
The mean number of students per classroom, y, at Central High School can be estimated using the equation y=0.8636x+27.227. where x represents the number of years since 2004 and x ≤ 10. Which of the following statements is the best interpretation of the number 0.8636 in the context of this problem?
Select the Correct Answer:
If 2/(a-1)=4/y where y ≠1, what is y in terms of
Select the Correct Answer:
if y=x^3 +2x+5 and z= x^2 + 7x+1, what is 2y+z in terms of x?
2x^3 + x^2 + 11x +11
Substituting the expressions equivalent to y and z into 2y +z results in the expression
2(x^3 +2x +5) +x^2+ 7x +1. The student must apply the distributive property to multiply
x^3 +2x +5 by 2
and then combine the like terms in the expression.
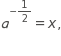
where a>0 and x>0, which of the following equations gives a in terms of x?
There are multiple ways to approach this problem, but all require an understanding of the properties of exponents. The student may rewrite the equation as 1/(a^0.5)=x
and then proceed to solve for a first by squaring both sides, which gives
(1/a)=x^2 and then multiplying both sides by a to find 1=a(x^2).Finally, dividing both sides by x^2 isolates the desired variable.
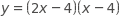
The graph of the eqution is a parabola in the xy-plane. In which of the following equivalent equations do the x- and y-coordinates of the vertex of the parabola appear as constants or coefficients?

Which of the following is equal to (14-2i)(7+12i)? (Note i=(-1)^0.5)
Select the Correct Answer:
In the equation above, what is the value of k?

Select the Correct Answer:
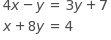
Based on the system of equations above, what is the value of the product xy?
There are several solution methods possible, but all involve persevering in solving for the two variables and calculating the product. For example, combining like terms in the first equation yields 4x - 4y = 7 and then multiplying that by 2 gives 8x -8y-14. When this transformed equation is added to the second given equation, the y-terms are eliminated, leaving an equation in just one variable:
9x = 18 ,or x =2.
Substituting 2 for x in the second equation (one could use either to solve) yields
2+8y =4 , which gives y =1 /4. Finally, the product xy is 2 * 1/4 =1/2.
if 0.5x+(1/3)y=4, what is the value of 3x+2y?
24
A student may find the solution to this problem by noticing the structure of the given equation and seeing that multiplying both sides of the equation 0.5x +(1/3)y =4 by 6 to clear fractions from the equation yields 3x +2 y =24.
Which of the following is equal to sin(π/5)?
Select the Correct Answer:
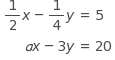
In the system of linear equations above, a is a constant. If the system has no solution, what is the value of a ?

Anise needs to complete a printing job using both of the printers in her office. One of the printers is twice as fast as the other, and together the printers can complete the job in 5 hours. The equation above represents the situation described. Which of the following describes what the expression 1/x represents in this equation?
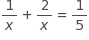
Select the Correct Answer:
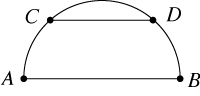
The semicircle above has a radius of r inches, and chord CD is parallel to the diameter AB. If the length of CD is (2/3) of the length of AB what is the distance between the chord and the diameter in terms of r?
Select the Correct Answer:
It is given that sinx= a, where x is the radian measure of an angle and π/2
Select the Correct Answer:
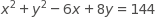
The equation of a circle in the xy-plane is shown above. What is the diameter of the circle?
26
Completing the square yields the equation (x-3)^2 +(y+4)^2 = 169.
the standard form of an equation of the circle. Understanding this form results in the equation r^2=169, which when solved for r gives the value of the radius as 13. The diameter is twice the value of the radius; therefore, the diameter is 26.




