Description
These are the following ways to calculate the area , where area for 2D shapes and Surface Area for 3D shapes
Study Set Content:
Circle
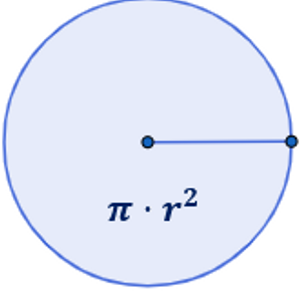
π × (r)^2
r = radius of the circle
Triangle
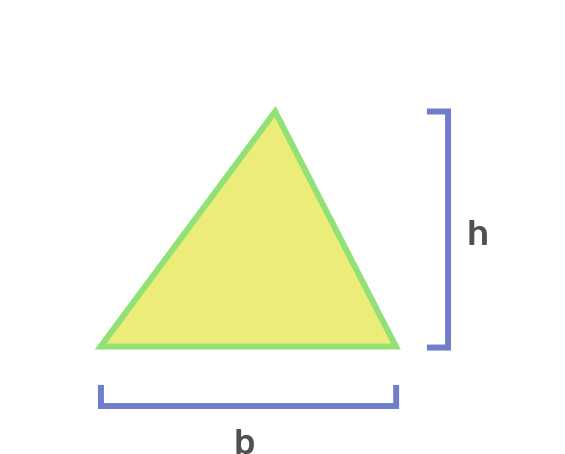
½ × b × h
b = base
h = height
Square
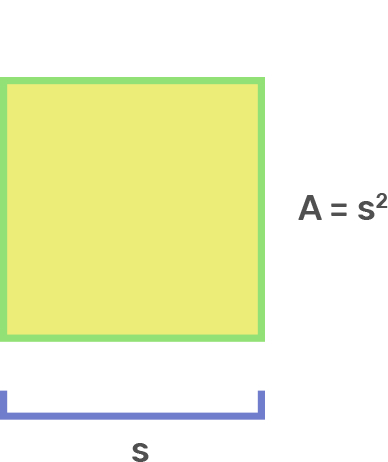
s^2
s = length of side
Rectangle
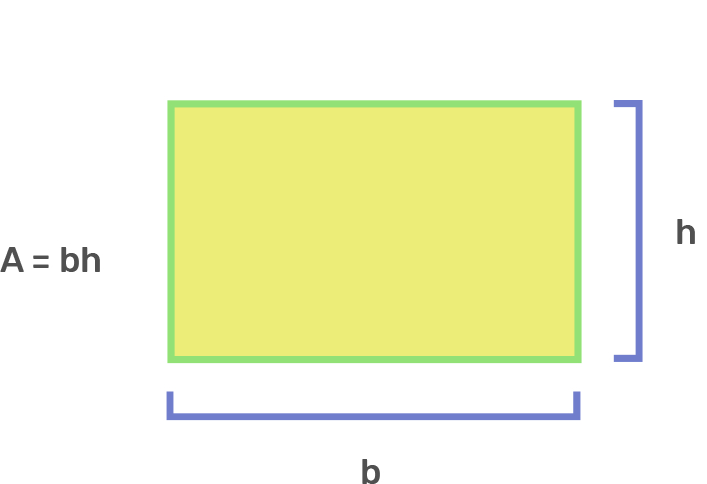
b × h
b = length
h = width
Parallelogram
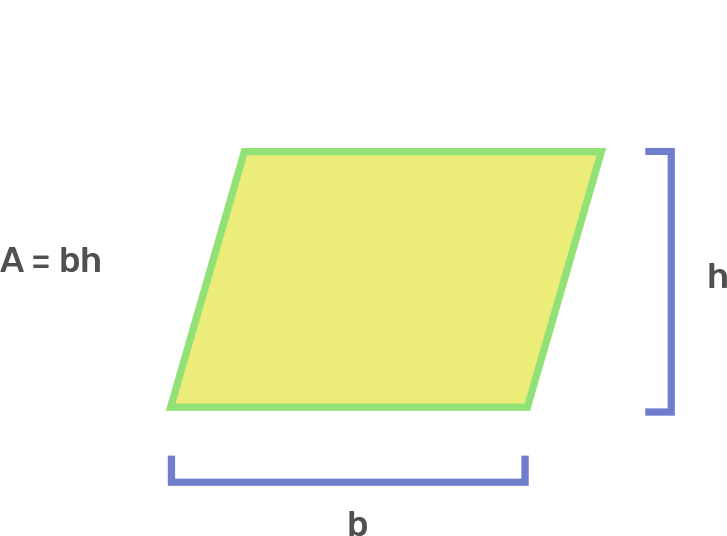
b × h
b = base
h = vertical height
Trapezium
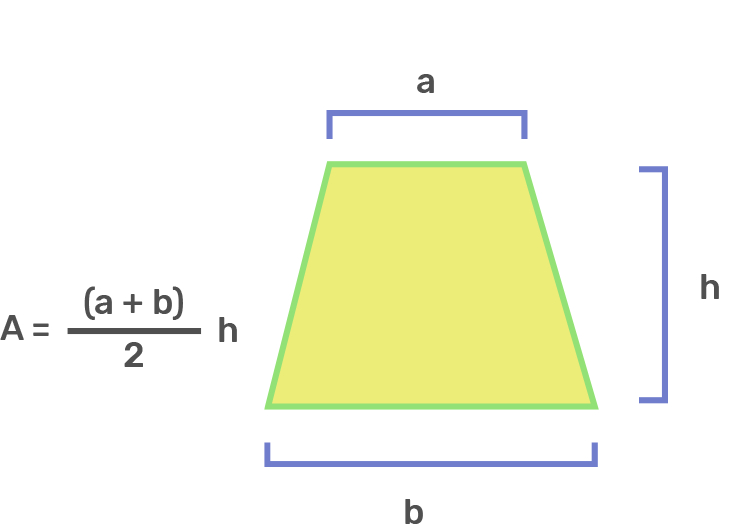
½(a + b) × h
a & b are length of parallel sides
h = height
Ellipse
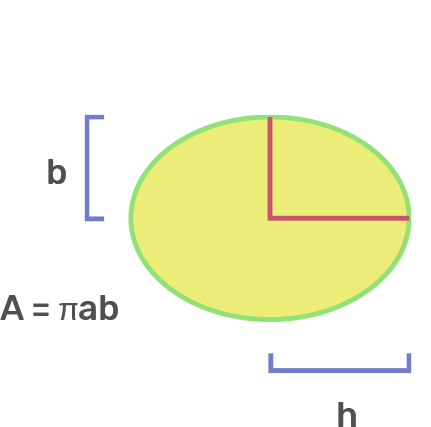
π×a×b
a = ½ minor axis
b = ½ major axis
Solid Sphere
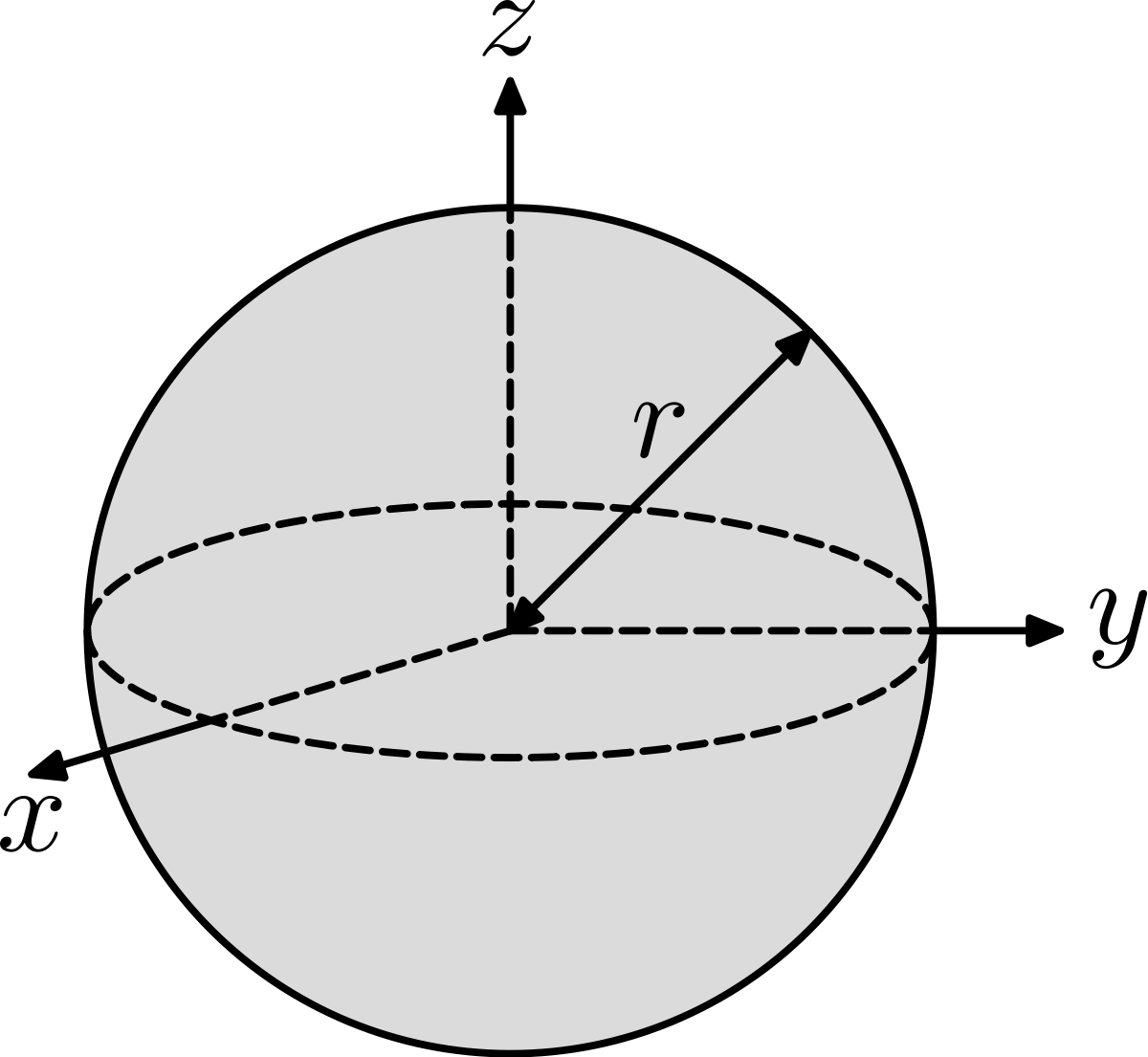
4 × π × r × r
r = radius
Hemisphere
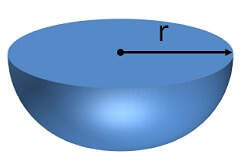
3 × π× r × r
r = radius
Right Prism
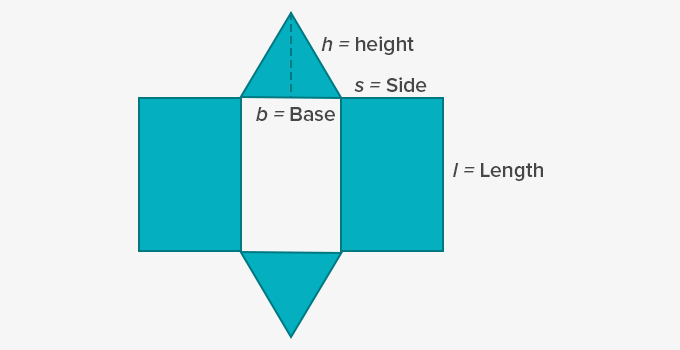
((b × h)+(2 × l × s)+(l × b))
S= side
l = Length
b = base
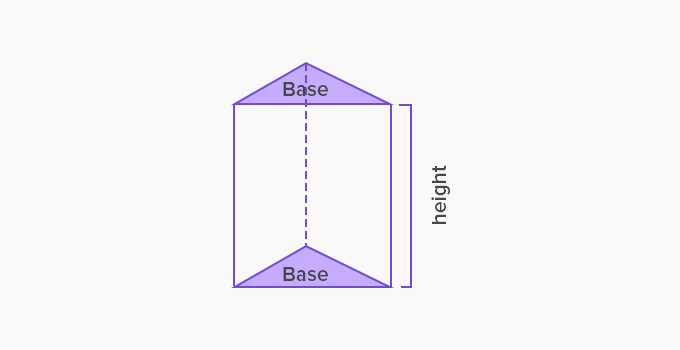
Right Prism
Height: The height is a lateral edge.
Side faces: Side faces are rectangles.
Surface Area: ((b × h)+(2 × l × s)+(l × b))
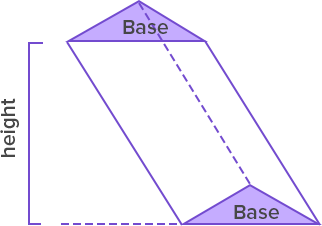
Oblique Prism
Height: Height is an altitude outside the prism.
Side faces:
Sides faces are parallelograms.
Surface Area= ((b × h)+(2 × l × s)+(l × b))
:
Cylinder
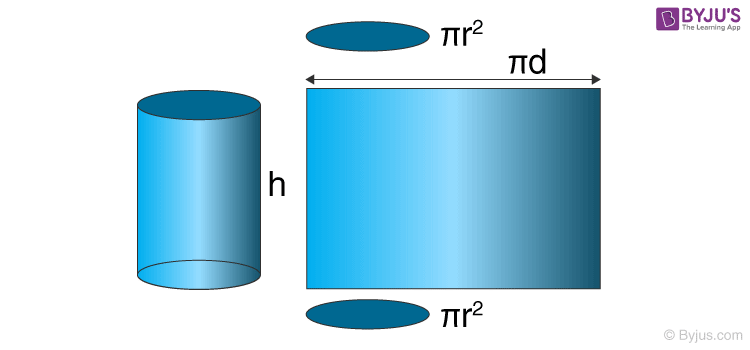
4 x π x r + 2 x h
r = Radius of the circular base of the cylinder
h = Height of the cylinder
