Study Set Content:
What are Algebraic Equations?
An algebraic equation is always a balanced equation that includes variables, coefficients, and constants.
In the form:
P = 0
Where P is a polynomial.
For example, x + 8 = 0 is an algebraic equation, where x + 8 is a polynomial. Hence, it is also called a polynomial equation.
What is an Equation?
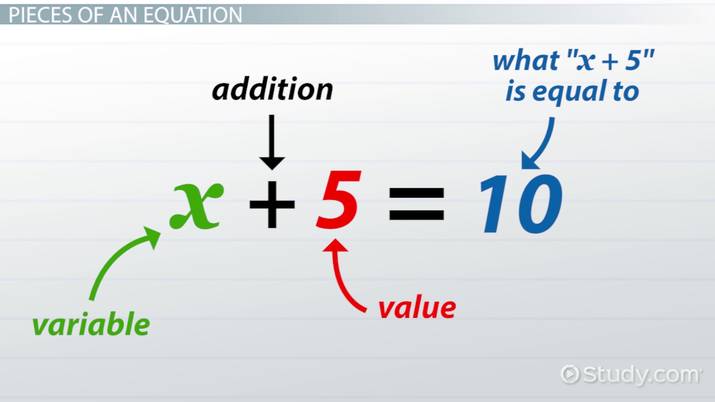
An equation is simply defined as mathematical statements that express the relationship between two values. Usually, the two values are equated by an equal sign in an equation.
Types of Algebraic Equations
-Polynomial Equations
-Quadratic Equations
-Cubic Equations
-Rational polynomial Equations
-Trigonometric Equations
Polynomial Equations Definition
The equations formed with variables, exponents and coefficients are called as polynomial equations. It can have different exponents, where the higher one is called the degree of the equation
Polynomial Equations Formula
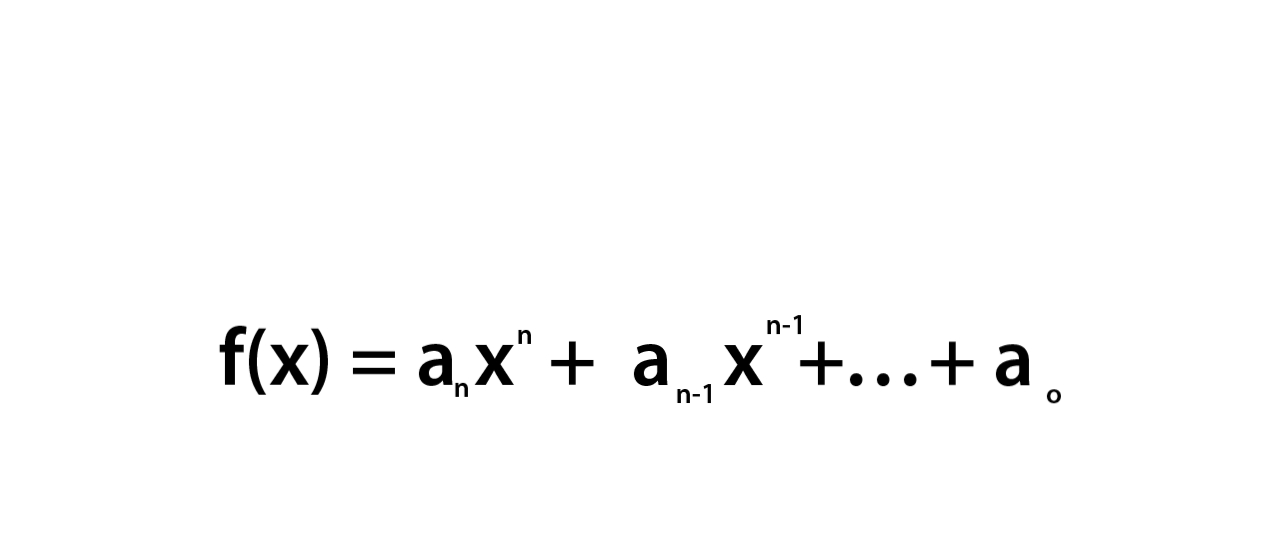
Types of Polynomial Equation
- Monomial Equations
- Binomial Equations
- Trinomial or Cubic Equations
- Linear Polynomial Equations
- Quadratic Polynomial Equations
- Cubic Polynomial Equation

Monomial Equation
An equation which has only one variable term is called a Monomial equation. This is also called a linear equation. It can be expressed in the algebraic form of;
ax + b = 0
Binomial Equations
An equation which has only two variable terms and is followed by one variable term is called a Binomial equation.
This is also in the form of the quadratic equation. It can be expressed in the algebraic form of;
a(x^2) + bx + c = 0

Trinomial Equations
An equation which has only three variable terms and is followed by two variable and one variable term is called a Trinomial equation.
This is also called a cubic equation. In other words, a polynomial equation which has a degree of three is called a cubic polynomial equation or trinomial polynomial equation.
Since the power of the variable is the maximum up to 3, therefore, we get three values for a variable, say x.
It is expressed as;
a(x^3) + b(x^2) + cx + d = 0
Quadratic Polynomial Equation
A polynomial equation which has a degree as two is called a quadratic equation. The expression for the quadratic equation is:
a(x^2) + bx + c = 0 ; a ≠ 0
Rational Polynomial Equations

P(x)/Q(x)=0
Trigonometric Equations
All the trigonometric equations are all considered as algebraic functions. For a trigonometry equation, the expression includes the trigonometric functions of a variable.
Trigonometric Equations: cos2x = 1+4sinx
Difference Between Expression and Equations

Many times students are confused between expressions and equation. Here is the difference between them
Trigonometric Ratios
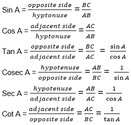
Trigonometric Ratios Formulas
Trigonometric Values For Standard Angles
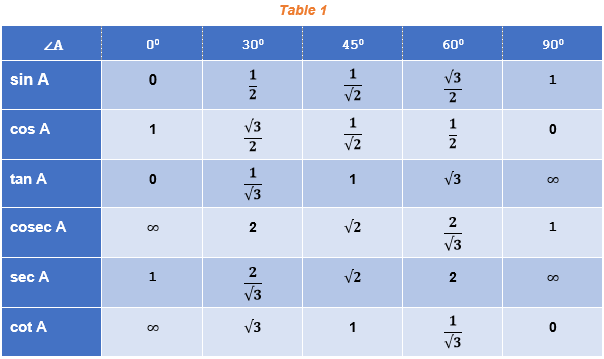
Each of the trigonometric ratios can be evaluated at different angles.
Some standard angles are given in this table for each of the ratios. From these standard angles, we can extend the evaluation of trigonometric ratios for any angles.
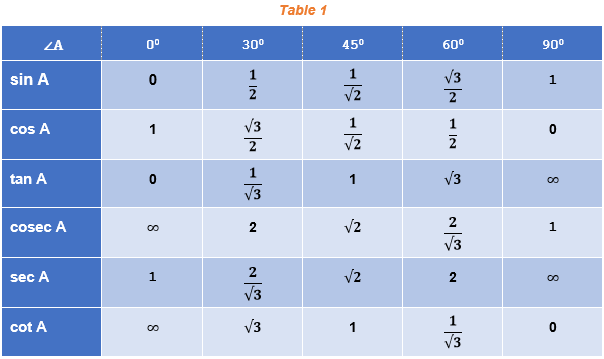
Remark
From the table 1 above, you can observe that as ∠ A increases from 0° to 90°, sin A increases from 0 to 1 and cos A decreases from 1 to 0.
Identities in Trigonometry
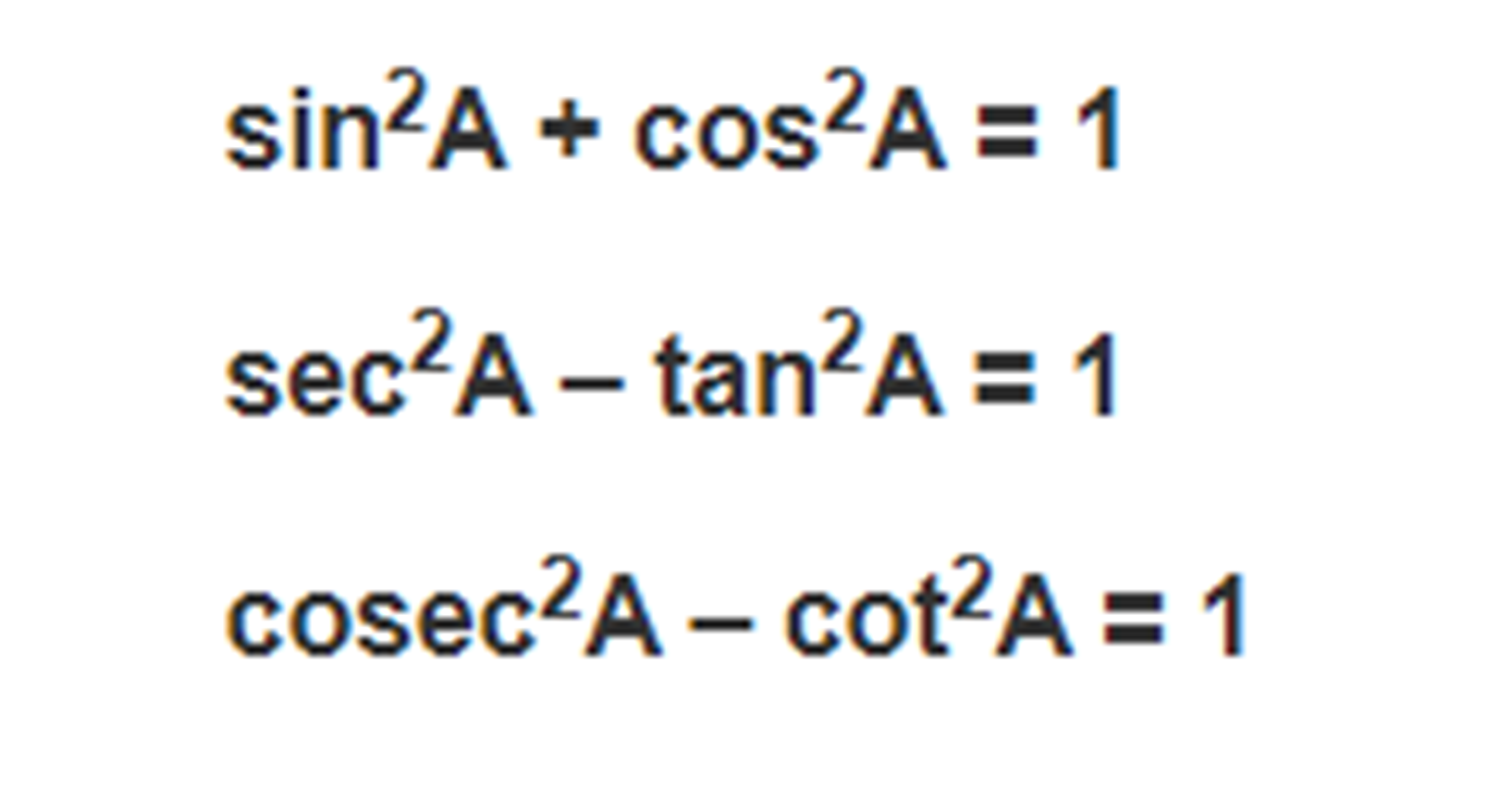
This is a very fundamental identity in trigonometry. Similarly, we can deduce other identities. They are listed here.
